So in summary:
Models with higher weights are unstable (have high variance) and can lead to large output changes for small input changes. So we want to keep weights low as much as possible.
This is done by regularization.
L2 regularization -> will encourage the weights to be close to zero but doesn't necessarily make some parameters/weights zero. So this will indeed decrease variance and reduce instability but by bringing weights close to zero not making them zero.
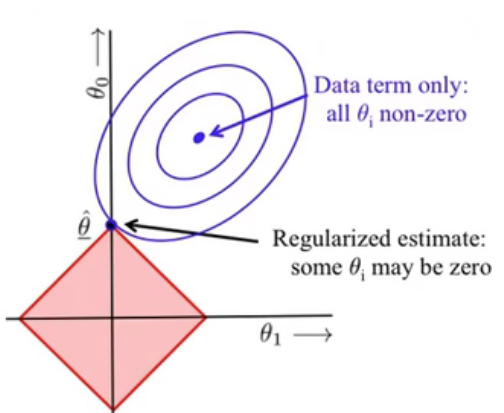
L1 regularization -> can encourage some weights to be zero so creates sparse parameters. say if we have p1 and p2 parameters, increase in p1 must be offset by decrease in p2.
L1
https://machinelearningmastery.com/weight-regularization-to-reduce-overfitting-of-deep-learning-models/
https://towardsdatascience.com/weight-decay-l2-regularization-90a9e17713cd
https://www.youtube.com/watch?v=sO4ZirJh9ds
Regularization basically adds the penalty as model complexity increases.
Does low weight mean low complexity?
A machine learning model is said to be complex when the model have so many Thetas that model memorizes everything in the data. Regularization penalizes the model for higher weights, thus driving some weights to zero.
A network with large network weights can be a sign of an unstable network where small changes in the input can lead to large changes in the output. This can be a sign that the network has overfit the training dataset. The weights will grow in size in order to handle the specifics of the examples seen in the training data.
Large weights make the network unstable. Although the weight will be specialized to the training dataset, minor variation or statistical noise on the expected inputs will result in large differences in the output. Generally, we refer to this model as having a large variance and a small bias.
Having small weights or even zero weights for less relevant or irrelevant inputs to the network will allow the model to focus learning. This too will result in a simpler model.
It is generally good practice to update input variables to have the same scale. When input variables have different scales, the scale of the weights of the network will, in turn, vary accordingly. This introduces a problem when using weight regularization because the absolute or squared values of the weights must be added for use in the penalty.
The smallness of weights implies that the network behaviour won’t change much if we change a few random inputs here and there which in turn makes it difficult for the regularized network to learn local noise in the data. This forces the network to learn only those features which are seen often across the training set.
We want to penalize all theta values to reduce the model complexity. But how does this help? How does it get rid of the parameter altogether?
The effect of regularization is that it decreases the number of possible hypotheses which are likely to be the final estimate, which in turn decreases the model capacity and reduces overfitting. You basically make the prior more sparse, which also makes the posterior more sparse.
A regression model that uses L1 regularization technique is called Lasso Regression and model which uses L2 is called Ridge Regression.
The L2-norm imposes a Gaussian prior, keeping all values near zero.
L1 encourages sparsity
The L1-norm imposes a Laplacian prior, allowing only a few parameters to be far from zero while the other parameters are forced to be near zero (which results in sparseness). sum should be 1, so if one parameter increases other decreases but this allows one param to be zero as well.
L1 Penalization works well when dealing with high dimensional data because its penalty parameter λ allows us to ignore or remove irrelevant features.
Ridge Regression allows us avoid overfitting by shrinking large coefficients towards zero and leaving small ones unchanged according to Tikhonov Regularization